Least-cost path analysis
If the shortest path
between any two points is a straight line, then the least-cost path is the path
of least resistance.
Least-cost path analyses
use the cost weighted distance and direction surfaces for an area to determine a
cost-effective route between a source and a destination. For example, you can
use least-cost path analysis to find the cheapest route for building a pipeline
or the quickest way to a set of observation points.
In a least-cost path
analysis, the eight neighbors of a cell are evaluated and the path moves to the
cell with the smallest accumulated value. The process repeats itself until the
source and destination are connected. The completed path represents the
smallest sum of cell values between the two points.
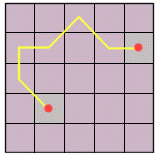
The least-cost path can travel through cells in both
orthogonal and diagonal directions.
Any combination of sources
and destinations can be part of a least-cost path analysis. For example, you
can find the least-cost path from one source to many
destinations, or from many sources to a single destination.
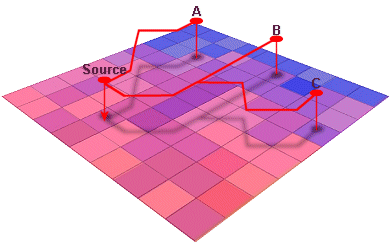
This example has one source and three destinations. The
least-cost path analysis uses both a cost weighted distance and direction
surface to find the most cost-effective route between each destination and the
source.