Map projections and distortion

Converting a sphere to a flat surface results in distortion. This is the most profound single fact about map projections—they distort the world—a fact that you will investigate in more detail in Module 4, Understanding and Controlling Distortion.

Imagine a map projection as an attempt to reconstruct your face in two dimensions. Some maps will get the shapes of all your features just right, but not the sizes—your forehead and chin, for instance, may come out huge. Other maps will get the sizes right, but the shapes will be stretched—maybe your full, round mouth will appear wide, thin, and rather mean.

Some maps preserve distances. Measurements from the tip of your nose to your chin, ears, and eyes will be right, even though the size and shape of your features is wrong. Other maps preserve direction. Your features may look weird, and they may be scrunched up or set too far apart, but their relative positions will be correct.

Finally, some maps are compromises—they get nothing exactly right but nothing too far wrong. In particular, compromise projections try to balance shape and area distortion.

So the four spatial properties subject to distortion in a projection are:

· Shape

· Area

· Distance

· Direction

Shape
If a map preserves shape, then feature outlines (like country boundaries) look the same on the map as they do on the earth. A map that preserves shape is conformal. Even on a conformal map, shapes are a bit distorted for very large areas, like continents.

A conformal map distorts area—most features are depicted too large or too small. The amount of distortion, however, is regular along some lines in the map. For example, it may be constant along any given parallel. This would mean that features lying on the 20th parallel are equally distorted, features on the 40th parallel are equally distorted (but differently from those on the 20th parallel), and so on.

Area
If a map preserves area, then the size of a feature on a map is the same relative to its size on the earth. For example, on an equal-area world map, Norway takes up the same percentage of map space that actual Norway takes up on the earth.

To look at it another way, a coin moved to different spots on the map represents the same amount of actual ground no matter where you put it.

In an equal-area map, the shapes of most features are distorted. No map can preserve both shape and area for the whole world, although some come close over sizeable regions.

Distance
If a line from a to b on a map is the same distance (accounting for scale) that it is on the earth, then the map line has true scale. No map has true scale everywhere, but most maps have at least one or two lines of true scale.

An equidistant map is one that preserves true scale for all straight lines passing through a single, specified point. For example, in an equidistant map centered on Redlands, California, a linear measurement from Redlands to any other point on the map would be correct.

Direction
Direction, or azimuth, is measured in degrees of angle from north. On the earth, this means that the direction from a to b is the angle between the meridian on which a lies and the great circle arc connecting a to b.

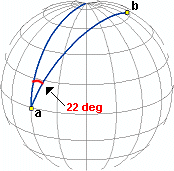
The azimuth of a to b is 22 degrees.

If the azimuth value from a to b is the same on a map as on the earth, then the map preserves direction from a to b. An azimuthal projection is one that preserves direction for all straight lines passing through a single, specified point. No map has true direction everywhere.

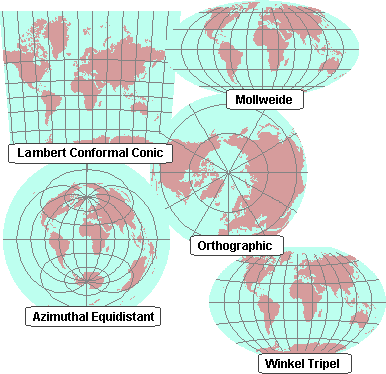
A few projections with different properties. The Lambert Conformal Conic preserves shape. The Mollweide preserves area. (Compare the relative sizes of Greenland and South America in one and then the other.) The Orthographic projection preserves direction. The Azimuthal Equidistant preserves both distance and direction. The Winkel Tripel is a compromise projection.

More about scale

Scale is the relationship between distance on a map or globe and distance on the earth.

Suppose you have a globe that is 40 million times smaller than the earth. Its scale is 1:40,000,000. Any line you measure on this globe—no matter how long or in which direction—will be one forty-millionth as long as the corresponding line on the earth. In other words, the scale is true everywhere. This is because the globe and the earth have the same shape (disregarding the complication of sphere versus spheroid).

Now suppose you have a flat map that is 40 million times smaller than the earth. (See the problem coming? Instead of comparing a big orange to a little orange, we're comparing a big orange to a little wafer.) This map also has a scale of 1:40,000,000, but because the map and the earth are differently shaped, this scale cannot be true for every line on the map.

The stated scale of a map is true for certain lines only. Which lines these are depends on the projection and even on particular settings within a projection. We'll come back to this subject in Module 4, Understanding and Controlling Distortion.

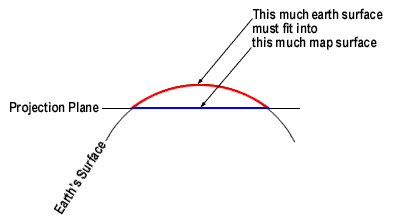
Not all of the earth's curves can be represented as straight lines at the same fixed scale. Some lines must be shortened (and others lengthened).

Expressing map scale
There are three common ways to express map scale:

Linear scales
Linear scales are lines or bars drawn on a map with real-world distances marked on them. To determine the real-world size of a map feature, you measure it on the map with a ruler or a piece of string. Then you compare the feature's length on the string to the scale bar.

A typical scale bar.

Verbal scales
Verbal scales are statements of equivalent distances. For example, if a 4.8 kilometer road is drawn as a 20 centimeter line on a map, a verbal scale would be “20cm = 4.8km.” You could also formulate the scale (reducing both sides by 20) as “1cm = .24km.”

Representative fractions
Representative fractions express scale as a fraction or ratio of map distance to ground distance. For example, a scale of 1:24,000 (also written 1/24,000) means that one unit on the map is equal to 24,000 of the same units on the earth. Since the scale is a ratio, it doesn't matter what the units are. You can interpret it as 1 meter = 24,000 meters, 1 mile = 24,000 miles, or 1 hand width = 24,000 hand widths (as long as it's the same hand).

Small scale and large scale maps
It's easy to mix these terms up. Here's one way to keep them straight: on a large-scale map, the earth is large (so not very much of it fits on the map). On a small-scale map, the earth is small (so all or most of it fits on the map). A map of your town, or your property, is going to be a large-scale map. A continental or world map is a small-scale map.

Another way to think of the difference in terms of representative fractions. The larger the fraction, the larger the map's scale. For example, 1/10,000 is a larger fraction than 1/1,000,000. So a 1:10,000 map is larger scale than a 1:1,000,000 map.

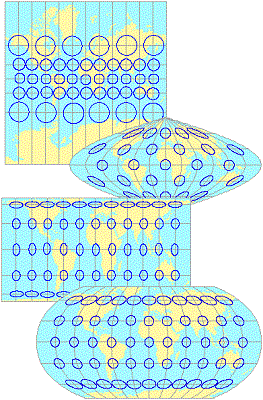
Measuring distortion using Tissot's Indicatrix

In the nineteenth century, Nicolas Auguste Tissot developed a method to analyze map projection distortion.

An infinitely small circle on the earth's surface will be projected as an infinitely small ellipse on any given map projection. The resulting ellipse of distortion, or indicatrix, shows the amount and type of distortion at the location of the ellipse.

For example, if an indicatrix is elongated from north to south, shape is correspondingly distorted at that location on the map. The same goes for east–west stretching or oblique stretching. On a conformal map, the indicatrices are all circles, but they vary in size. On an equal area projection, the indicatrices have varying ellipticity, but the same area.

The Mercator projection is conformal. All indicatrices are circles; area distortion varies with latitude. The Sinusoidal projection preserves area. All indicatrices enclose the same area.; shapes are obliquely distorted. The Equal-Area Cylindrical projection also preserves area. Shapes are distorted from north to south in middle latitudes and from east to west in extreme latitudes. In the Robinson projection, neither shape nor area is perfectly right anywhere. Both properties are nearly right in middle latitudes.

Tissot indicatrices for four projections.