What is interpolation?
Interpolation is the
process of estimating unknown values that fall between known values.
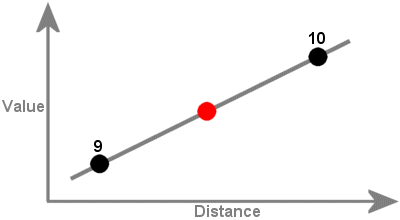
In this example, a
straight line passes through two points of known value. You can estimate the
point of unknown value because it appears to be midway between the other two
points. The interpolated value of the middle point could be 9.5.
Spatial interpolation
calculates an unknown value from a set of sample points with known values that
are distributed across an area. The distance from the cell with unknown value
to the sample cells contributes to its final value estimation.
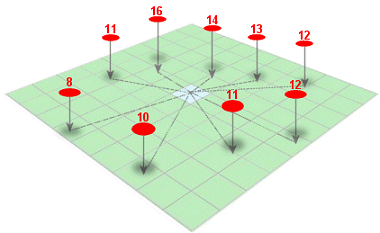
The unknown value of
the cell is based on the values of the sample points as well as the cell's
relative distance from those sample points.
You can use spatial interpolation
to create an entire surface from just a small number of sample points; however,
more sample points are better if you want a detailed surface.
In general, sample points
should be well-distributed throughout the study area. Some areas, however, may require
a cluster of sample points because the phenomenon is transitioning or
concentrating in that location. For example, trying to determine the size and
shape of a hill might require a cluster of samples, whereas the relatively flat
surface of the surrounding plain might require only a few.
Whether you are concerned
with the amount of rainfall, concentrations of pollution, or the differences in
elevation, it is impossible to measure these phenomena at every point within a
geographic area. You can, however, obtain a sample of measurements from various
locations within the study area, then, using those samples, make inferences
about the entire geographic area. Interpolation is the process that enables you
to make such an inference.
The primary assumption of
spatial interpolation is that points near each other are more alike than those
farther away; therefore, any location's values should be estimated based on the
values of points nearby.
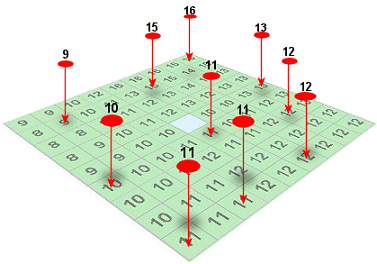
Interpolating the sample points' values creates a surface.
As with all of the cells, the unknown value of the light-blue
cell in the center will be estimated based on values of the surrounding sample
points.
With spatial interpolation, your
goal is to create a surface that models the sampled phenomenon in the best
possible way. To do this, you start with a set of known measurements and, using
an interpolation method, estimate the unknown values for the area. You then
make adjustments to the surface by limiting the size of the sample and
controlling the influence the sample points have on the estimated values.