Least-cost path analysis

If the shortest path between any two points is a straight line, then the least-cost path is the path of least resistance.

Least-cost path analyses use the cost weighted distance and direction surfaces for an area to determine a cost-effective route between a source and a destination. For example, you can use least-cost path analysis to find the cheapest route for building a pipeline or the quickest way to a set of observation points.

In a least-cost path analysis, the eight neighbors of a cell are evaluated and the path moves to the cell with the smallest accumulated value. The process repeats itself until the source and destination are connected. The completed path represents the smallest sum of cell values between the two points.

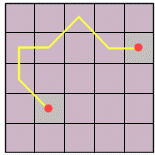
The least-cost path can travel through cells in both orthogonal and diagonal directions.

Any combination of sources and destinations can be part of a least-cost path analysis. For example, you can find the least-cost path from one source to many destinations, or from many sources to a single destination.

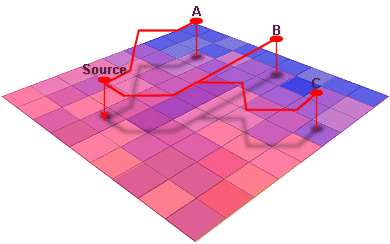
This example has one source and three destinations. The least-cost path analysis uses both a cost weighted distance and direction surface to find the most cost-effective route between each destination and the source.