Triangulated Irregular Network (TIN)

A Triangulated Irregular Network (TIN) represents space using a set of non-overlapping triangles that border one another and vary in size and proportion.

TINs are created from a set of input points with x, y, and z values. When you create a TIN, the input points become the triangle vertices (nodes). The vertices are connected by lines that form the triangle boundaries (edges). The final product is a continuous surface of triangles, made of nodes and edges.

Two images of the same TIN. Top: Only the TIN edges are shown. Bottom: The TIN's triangles (faces) are colored to represent elevation.

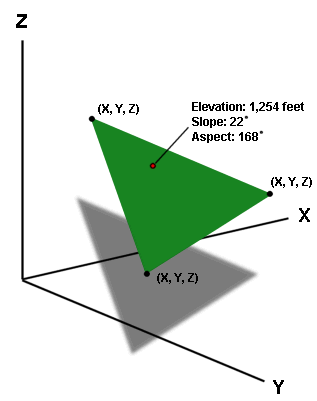
Once the TIN is built the elevation of any location on a TIN surface can be interpolated (i.e, mathematically estimated) using the x, y, and z values of the bounding triangle's vertices. The slope and aspect for each triangle face is also calculated.

The x,y, and z values are stored by the triangle nodes of a TIN. When you identify a point on a TIN, the node values are used to interpolate the elevation at that point. The node values are also used to calculate the slope and aspect of each triangle face.