Natural
Neighbors
A rich duke with 100 children
decides to divide his property in an unusual way. First, he tells each child to
stand somewhere (anywhere they like) on the property. When each child has found
a spot, a team of surveyors comes and marks every square of ground according to
the child closest to it. For instance, each piece of ground that is closer to
Child 43 than to any other child is marked with a 43; each piece that is closer
to Child 57 than to anyone else is marked with a 57, and so on.
When the process is finished, each
child stands inside a boundary, drawn with chalk, that
marks the land that is closer to him or her than to anyone else. This is the
property he or she inherits.
If you think of these children as a
set of points, the lines drawn around their properties would be Voronoi polygons. Voronoi
polygons are important in Natural Neighbors interpolation.
After a long afternoon’s work,
the entire property has been divided. Suddenly, the duke’s young wife shows up and announces that she is pregnant with his 101st
child. She demands that this child, too, receive a share of the inheritance.
The duke, with a sigh, tells her to
pick a spot of ground and stand on it. The surveyors redraw the property lines.
They don’t have to start from the beginning—they just have to
reshape the boundaries in the area around the duke’s wife. Now she, too,
stands inside her own Voronoi polygon. Its area is
made up of (or “stolen” according to the disgruntled children)
parts of the half dozen or so polygons around her.
Think of the pregnant duchess as an
estimation location. The six children—think of them as points—who
had some of their property taken away are the "natural neighbors" of
the estimation location. (There can be more or less than six, but six turns out
to be a common number.)
Now forget about the duke and his
children so we can talk about z-values without overloading the metaphor. In
Natural Neighbors interpolation, the value of an estimated location is a
weighted average of the values of the natural neighbors. The weighting is
proportional to the area in the estimation location’s Voronoi
polygon that was contributed by each natural neighbor’s polygon.
Since the output is a
raster, the estimation locations are a regularly-spaced array equal to the
number of raster cells.
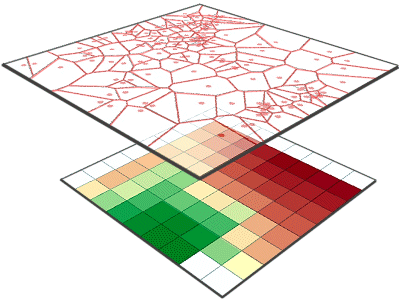
Top: Voronoi polygons are
constructed from the set of input points. Bottom: For each cell in the output
raster, a weighted average of the cell center's natural neighbors is
calculated.
![]() The Natural
Neighbors Nitty Gritty
The Natural
Neighbors Nitty Gritty
You may recall that a
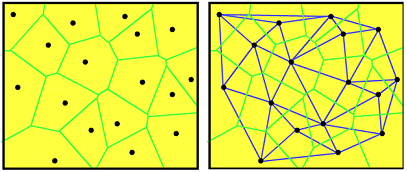
Left: Voronoi
polygons for a set of input points. The boundary around each point encloses the
area that is closer to that point than to any other point. Right: Voronoi polygons are closely related to Delaunay
triangles. Polygon sides bisect triangle edges.
To estimate an unknown
value at any location, such as the pink dot in the following graphic, a new Voronoi polygon is created for the location. The new
polygon encroaches on the surrounding polygons. The input points that belong to
these surrounding polygons are the natural neighbors of the point being
estimated.
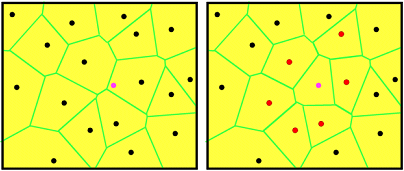
Left: The location to be
estimated is marked by the pink dot. Right: the red points are the natural
neighbors of the estimation location.
The value of the estimation
location is a weighted average of the natural neighbor values.
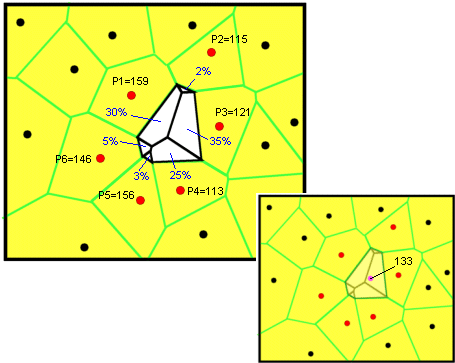
Top left: The new Voronoi polygon is analyzed according to what percentage of
its area came from each of the original polygons. The percentages are weights
that are multiplied by the values of the Natural Neighbors. Bottom right: the
value for the estimation location is 133. This is equal to (159*.3) + (115*.02)
+ (121*.35) + (113*.25) + (156*.03) + (146*.05.