Tissot indicatrices
Now you
know something about spatial distortion, but it would be nice to know a little
more—like which properties a particular projection distorts and how much.
A good
technique for evaluating distortion is the Tissot Indicatrix.
The idea is
that when a circle on a sphere is projected onto a flat surface, it is deformed
into an ellipse. The size, shape, and orientation of this ellipse (which is
called an indicatrix) describes
the spatial distortion at that location. By placing indicatrices
at regular intervals, you can see the distortion pattern across the surface.
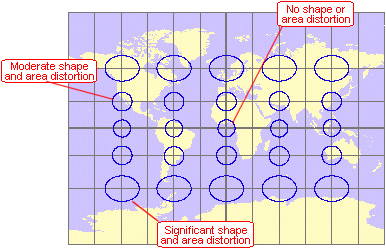
The Miller Cylindrical
projection is neither conformal nor equal area. There is no distortion of shape
or area along the equator, but both properties are increasingly distorted
toward the poles.
How big is an indicatrix?
Infinitely small. You can't directly compare a
spherical figure (like a circle on the earth's surface) to a plane figure (like
a projected ellipse). To compare them, you have to treat the circle as a plane
figure, and you do this by making it infinitely small. An infinitely small
circle doesn't work as a visual aid, so for practical purposes you have to draw
it bigger. The size you choose is arbitrary—what matters is that the projected
ellipse is drawn in correct proportion to it.
Here's
another example:
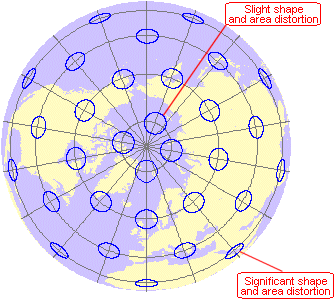
In the Orthographic
projection (polar aspect), there is a single point of no distortion at the north pole. (This point is not marked with an indicatrix.) Shape and area are increasingly distorted with
distance from the center; in this case, area shrinks relative to its true size.
Beyond a single hemisphere, severe distortion makes the projection unusable.
Tissot indicatrices aren't the only device for analyzing map
distortion. Another technique is to use isolines to
connect points of equal distortion (just as contour lines connect points of
equal elevation). This course, however, relies on the good offices of Monsieur Tissot. In the next concept, we'll take a deeper look at
his indicatrices.
Quantifying distortion
Tissot indicatrices can give you a good general sense of
distortion. But you might want to know just how good “good” is. You can also
use the indicatrix to quantify distortion at any
point on a map.
Below is a
more detailed drawing. The blue ellipse is the Tissot
indicatrix. The green circle is a reference circle
representing the original figure on the sphere.
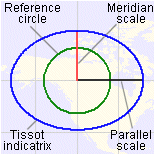
The graphic elements of
a Tissot indicatrix.
Area
distortion
The indicatrix is larger
than the reference circle and differently shaped. This tells you that both area
and shape are distorted at this location. (If there were no distortion, the indicatrix and the circle would be identical.)
It's easy
to see that area is distorted, but by how much? Would you say the ellipse is
twice as big as the reference circle? Three times as big?
Four?
![]() Check the area distortion
Check the area distortion
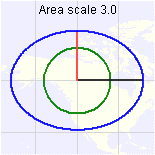
At this location (60°N,
120°W) on a Miller Cylindrical projection, area is shown three times larger
than its true size. Remember, the "area" we're talking about is that
of an infinitely small ellipse, not the whole area covered by the graphic.
Distance
distortion
The red line on the indicatrix
represents scale (distance) along the meridian. The black line represents scale
along the parallel. When either line goes past the green reference circle—or
doesn't reach it—there is distance distortion along that line. Here, both
scales are exaggerated, though by different amounts. (In fact, scale is exaggerated
here in all directions, since any line drawn from the center of the
circle to the ellipse would go beyond the reference circle.)
If you
define the length of the reference circle's radius as 1 unit, then a scale
factor of 1.0 along a given line means there is no scale distortion in that
direction. (A scale factor of 2.0 along a given line means that the line's
length is twice the radius of the reference circle.)
In the
graphic above, what would you estimate the scale factor along the meridian to
be? About 1.5? How about the scale factor along the
parallel?
![]() Check the scale factor
Check the scale factor
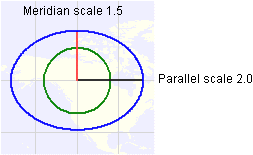
In this graphic, the
scale factor along the meridian is, in fact, 1.5. The scale factor along the
parallel is 2.0.
Shape
distortion
Shape distortion is measured by angular deformation. Consider a pair of
intersecting lines on a reference circle. When those lines are projected, the
angle between them on the Tissot indicatrix
will be different than it was on the reference circle (assuming the map is nonconformal and the lines don't happen to be the major and
minor axes of the indicatrix).
Remember
the following graphic from the Shape concept?
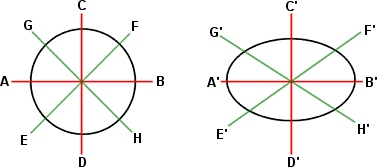
The angles formed by
intersecting lines change when a reference circle is projected to an ellipse.
At each
location, one pair of lines will undergo a greater change in angle than any
other pair. This greatest angular change, measured in degrees, is called the maximum
angular deviation (or deformation). If the location is conformal, this
value is 0. (On a conformal map, it is 0 at all locations). If the location is nonconformal, this value varies from a few degrees (low
distortion) to more than 90 degrees (severe distortion).
![]() What about distortion of direction?
What about distortion of direction?
Distortion of this property can't be analyzed from a Tissot indicatrix.
Useful indicatrix measures
Location : The latitude-longitude coordinates
of the location being analyzed.
Parallel
scale: The scale
factor along the parallel. A value of 1.0 means there is no distance distortion
along the parallel. Values greater than one mean that the map
overstates the true distance. Values less than one
mean that the map understates the true distance.
![]() More about parallel scale
More about parallel scale
Suppose you make a measurement along a given parallel.
According to your map's scale bar, the distance you measured is 100 kilometers.
That's true only if the parallel scale at that location is 1.0. If the parallel
scale is 2.0, then the true distance is 50 kilometers. If the parallel scale is
0.5, then the true distance is 200 kilometers.
Meridian scale: The scale factor along the
meridian. A value of 1.0 means there is no distance distortion along the
meridian.
Maximum scale: The greatest scale factor in any
direction (always the direction of the major axis of the indicatrix.).
A value of 1.0 means that scale is true along the major axis and is not
overstated in any direction.
Minimum scale: The smallest scale factor in any
direction (always the direction of the minor axis of the indicatrix).
A value of 1.0 means that scale is true along the minor axis and is not
understated in any direction.
Area scale: The maximum scale multiplied by
the minimum scale. A value of 1.0 means there is no area distortion. Values greater than one mean that the map overstates the true area.
(For example, a value of 4.0 means that the map shows area as four times larger
than it really is.) Values less than one mean that the map
understates the true area.
Meridian-parallel angle: The projected angle between the
meridian and the parallel. A value of 90 means that this angle is not
distorted.
Maximum angular deviation: The greatest angular change in any
pair of intersecting lines when a reference circle is projected. A value of 0 means that the location is conformal.