Shape
A conformal
map preserves the property of shape, so feature outlines on the map are the
same as they are on a globe or on the earth.
Mathematically,
shape is a matter of angles. In the graphic below, the red lines AB and CD
represent the axes of a circle on the earth’s surface. They intersect at 90
degree angles. A pair of perpendicular green lines inclined
at 45 degrees to the red lines also make 90 degree angles. The same goes
for any pair of perpendicular lines that intersect at the center of the circle.
If all
these angles stay the same when the circle is projected onto a map, then the
map is conformal. A conformal map preserves angles.
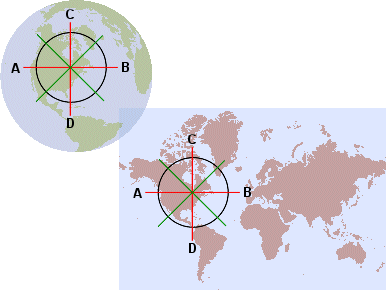
A circle on a sphere
and the same circle projected onto a conformal map. The mathematics described
above actually apply to infinitely small circles, not
to the very large circles shown here.
The fact
that a map is conformal doesn't mean it has uniform scale. (No map does.)
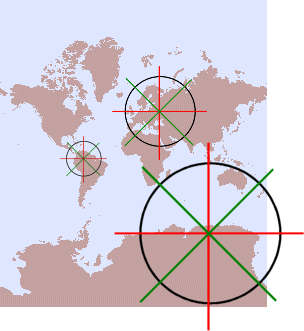
The Mercator
projection is conformal. Angles are not changed by the projection process.
Scale, on the other hand, is changed a lot. As you move from the equator to the
poles, distance and area is increasingly distorted.
Look what
happens to a circle when it is projected onto a non-conformal map—it becomes an
ellipse.
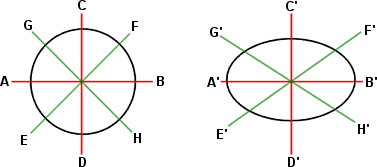
On the left, AB and CD
make 90 degree angles. So do their projected counterparts A'B' and C'D' on the
right. On the left, perpendicular lines EF and GH also make 90 degree angles.
However, their projected counterparts E'F' and G'H' do not.
In the
graphic above, the projected ellipse is stretched from side to side. (It could
have been stretched from top to bottom or in an oblique direction.) In any
case, there is only a single pair of intersecting lines on the ellipse whose
angles are not distorted. These lines are the major and minor axes.
Back in
Module 2, Flattening the Earth, you learned that conformality
breaks down for large regions, like continents. A planar shape can't be
faithful to a spherical shape at large sizes because
their mathematical properties are different. (For example, a triangle drawn on
a sphere has more than 180 degrees.) That's why conformal maps are often
described as “preserving angles locally” or “maintaining local angular
relationships.”