Choosing a projection
Even with
all you've learned about map projections, you may feel that you still don't
know how to pick a good one—that is, a projection that meets your needs. So
what makes a projection good? Two main things.
First, if
your map requires that a particular spatial property be held true, then a good
projection must preserve that property. In the first concept of this topic,
you'll look at this issue in more detail.
Second, a
good projection minimizes distortion in your area of interest. This issue is
complicated (for instance, are all types of distortion equally important?) and
also too mathematical to be explored in great detail. But the second and third
concepts in this topic will present some fairly simple and useful rules.
Most of the
time, it's not that hard to pick a good projection. Apart from what you'll
learn in the rest of the topic, here are a few points to keep in mind:
·
ArcMap can help. ArcMap has a large number of predefined projections organized by world,
continent, and country. You can navigate quickly to appropriate projections for
any part of the world.
·
Distortion is often insignificant. When you're working at large scales—for example,
provinces or districts within countries—distortion doesn't play a significant
role, and almost any projection that is centered on your area of interest is
okay. To put it more picturesquely, you can't flatten a beachball without a lot
of distortion, but you can flatten a postage stamp on a beachball.
·
You're not stuck with a bad choice. It's easy to change projections and to modify
projection parameters in ArcMap. So it's almost never too late to correct a
flawed choice.
·
You don't always have to choose. You may be working on a project or for an organization
where the question of which map projection to use has already been decided. For
example, the State Plane and UTM coordinate systems are established standards
for many large and medium-scale maps of
Concepts
What is the map's purpose?
When you
choose a projection, the first thing to consider is the purpose of your map.
For general reference and atlas maps, you usually want to balance shape and
area distortion. If your map has a specific purpose, you may need to preserve a
certain spatial property—most commonly shape or area—to achieve that purpose.
Maps
that preserve shape
On a conformal projection, all local angles measured from a point are correct
and all local shapes are true. You should use a conformal projection when the
map's main purpose involves measuring angles, showing accurate local
directions, or representing the shapes of features or contour lines. This
category includes:
·
Topographic
maps and cadastral (land parcel) maps
·
Navigation
charts (for plotting course bearings and wind direction)
·
Civil
engineering maps
·
Military
maps
·
Weather
maps (for showing the local direction in which weather systems are moving)
Click each of the maps
above to learn more about them and the projections they are in.
Most of the
maps in the list above would be large or medium-scale. In fact, most
large-scale maps nowadays are conformal, regardless of their purpose.
![]() Why are most large-scale
maps conformal?
Why are most large-scale
maps conformal?
At large scales, a conformal projection centered on the area
of interest produces insignificant errors in distance and area. These errors
are often smaller than what D.H. Maling, author of Coordinate Systems and
Map Projections, calls the "zero dimension"—the point at which
projection distortion is less than the error caused by physical properties of
the map (paper shrinkage, pen width, and so on).
"Large-scale" is not an exact term, but in this
context it should hold for scales of 1:100,000 or larger. It may also apply to
smaller scales if the area of interest has a compact shape. For example, Maling
says that the area distortion in a 1:500,000 Transverse Mercator projection of
Maps
that preserve area
On an equal-area projection, the size of any area on the map is in true
proportion to its size on the earth. You should use equal-area projections to
show:
·
The
density of an attribute with dots (for example, population density)
·
The
spatial extent of a categorical attribute (for example, land use maps)
·
Quantitative
attributes by area (for example, Gross Domestic Product by country)
Equal-area
maps have also been used as world political maps to correct popular
misconceptions about the relative sizes of countries.
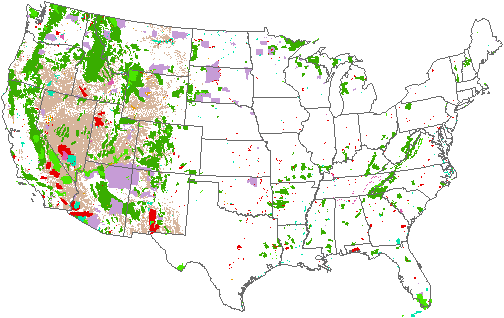
Dot density map of
federally-owned and Indian land in the
![]() Why equal-area
projections are essential for dot-density maps?
Why equal-area
projections are essential for dot-density maps?
Dot-density maps show the concentration of an attribute in
an area. The map of world population density you looked at before (shown again
below) uses one dot to represent every one million people. If areas are not in
true proportion, the map will give false impressions. Countries that draw
larger than their true area scale will look less dense than they should.
Countries that draw smaller than their true area scale will look too dense.
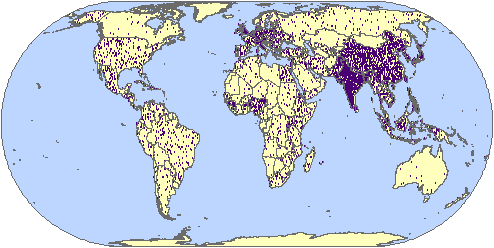
The Eckert
IV projection applied here is used by the National Geographic Atlas, 7th
edition, for several of its world thematic maps.
Maps
that preserve scale
No map provides true-to-scale distances for any measurement you might make. The
Azimuthal Equidistant projection preserves true scale from a single
specified point on the projection to all other points on the map. Possible
uses for this property include:
·
Maps
of airline distances from a single city to several other cities
·
Seismic
maps showing distances from the epicenter of an earthquake
·
Maps
used to calculate costs or charges based on straight-line distance from a
source
·
Maps
used to calculate ranges; for example, the cruising ranges of airplanes or the
habitats of animal species
The
Two-Point Equidistant projection preserves true scale from two specified
points on the projection to all other points on the map. This projection
could be used to determine the distance of a ship at sea from the start and end
of a voyage.
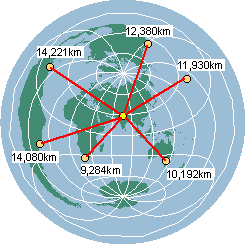
An Azimuthal Equidistant
projection centered on
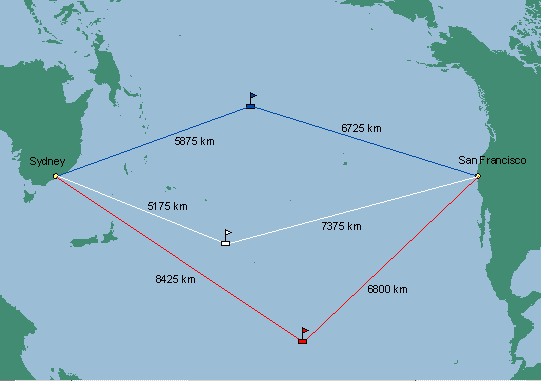
A Two-Point Equidistant
projection. Scale is correct from both
Maps
that preserve direction
On any azimuthal projection, all azimuths, or directions, are true from a
single specified point to all other points on the map. (On a conformal
projection, directions are locally true, but are distorted with distance.)
Direction is not typically preserved for its own sake, but in conjunction with
another property.
In
navigation and route planning, however, direction matters for its own sake. The
Gnomonic projection is unique among azimuthals in that every straight line
drawn on it represents the arc of a great circle. Since a great circle is the
shortest distance between two points, Gnomonic projections are useful for
planning air and sea routes and for mapping phenomena, like radio waves, that
follow shortest-distance paths.
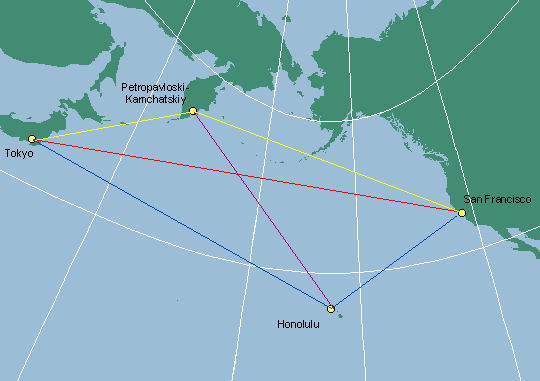
A Gnomonic projection.
Every straight line on the map is the shortest distance between two points. The
lines do not have true scale, however.
![]() True direction and
constant direction revisited
True direction and
constant direction revisited
On the Gnomonic projection, any straight line between two
points is the arc of a great circle. While good for route planning, this
property is not good for practical navigation, because to follow a great
circle, you have to keep changing your bearings.
On the Mercator projection—which is not azimuthal—any
straight line between two points is a line of constant bearing: you follow a
single compass heading to get from one point to another, but the route is
longer than a great circle.
For short routes, navigators rely on the Mercator. For long
routes, they may plan their course on the Gnomonic, then convert the great
circle path to a series of shorter rhumb lines on the Mercator.
General
purpose maps
Many compromise projections have been developed to show the world with a
balanced distortion of shape and area. Among the most successful are:
·
Winkel
Tripel (currently used by the National Geographic Society for world atlas maps)
·
Robinson
·
Miller
Cylindrical
For
larger-scale maps, from continents to large countries, equidistant projections
(equidistant in the sense of true scale along the meridians) are good at
balancing shape and area distortion. Depending on your area of interest, you
might use:
·
Azimuthal
Equidistant
·
Equidistant
Conic
·
Plate
Carrée
The
National Geographic Society uses the Two-Point Equidistant projection to
balance shape and area distortion for some maps of
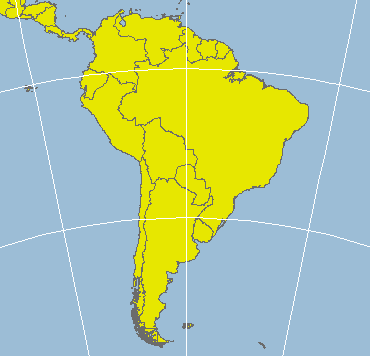
An Equidistant Conic
projection of
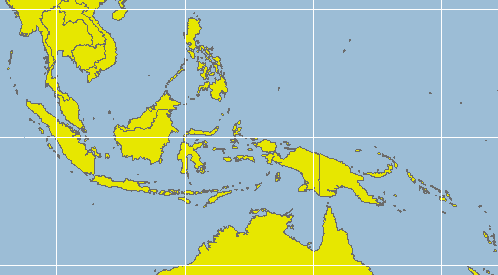
A Plate Carree projection
of
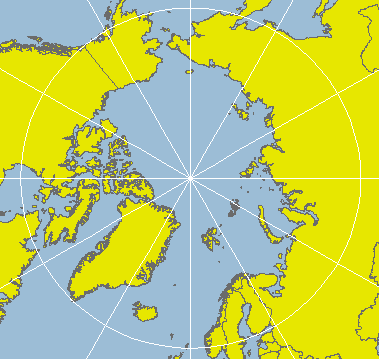
An Azimuthal Equidistant
projection of the north pole.
Which part of the world does your map show?
The map's
purpose narrows your choices, but doesn't determine a projection. After all,
there are many conformal projections, many equal-area projections, and many
compromise projections.
The next
step in choosing a projection is to decide on the class of projection:
cylindrical, conic, or azimuthal. A time-honored rule–dating to the 16th
century–is to choose according to the latitude of your area of interest. The
rule says:
·
To
map tropical regions, use a cylindrical projection
·
To
map middle latitudes, use a conic projection
·
To
map a polar region, use an azimuthal projection
The rule
makes sense if you think about the line (or point) of zero distortion for each
class of projection. In cylindrical projections, the line of zero distortion is
the equator; in conic projections, it's a parallel of latitude; in azimuthal
projections, it's one of the poles. Using a projection from the right class
minimizes distortion for your area of interest.
But the
rule applies only to the normal aspect of projections. For example, a
cylindrical projection, free of distortion along the equator, obviously makes a
better map of the tropics than an azimuthal projection centered on the north
pole. But does it make a better map than an oblique azimuthal projection centered
on the equator? Not necessarily.
The
latitude rule meant a lot before the computer age, when cartographers worked
from base maps drawn in a limited number of standard projections. Changing
aspect or standard lines could take weeks or months of work and might be hard
to justify for the sake of experimental or limited use. Nowadays, computer
software makes it easy to change aspect and to modify projection parameters so
that different classes of projection can be optimized for an area of interest.
![]() Does the latitude rule
still matter?
Does the latitude rule
still matter?
It's still a good rule of thumb, especially if you want to
choose a projection quickly and not worry about customizing the parameters.
Just don't think of the rule as a limitation on your options.
What shape is your area of interest?
Although
the latitude rule you just read about is less important than it used to be, the
idea behind it—that of minimizing distortion for your area of interest—is still
relevant. Azimuthal, conic, and cylindrical projections each have a distinct
pattern of distortion.
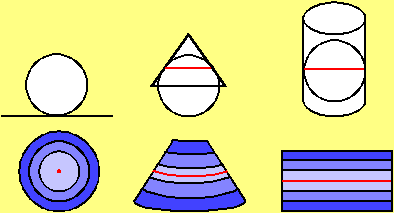
Top row: Conceptual
drawings of tangent azimuthal, conic, and cylindrical projections. Bottom row:
The corresponding distortion patterns. Darker blue shading represents
increasing distortion. Black lines represent lines of equal distortion. Red
points and lines represent zero distortion. Distortion contours for secant
projections are much the same.
So a useful
selection principle is to match the shape of your area of interest to a
distortion pattern. The old latitude rule has been given a new formulation by
Frank Canters, author of Small-scale Map Projection Design, (in slightly
different words than these):
·
To
map areas that extend along a great circle, use a cylindrical projection
·
To
map areas that extend along a small circle, use a conic projection
·
To
map areas that are approximately circular (or have equal extent in all
directions), use an azimuthal projection
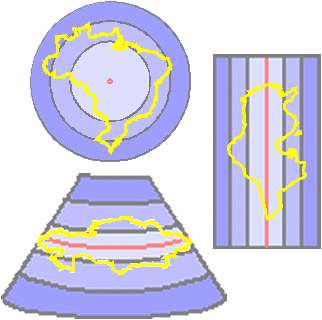
It's not
always easy to tell which distortion pattern is best-suited to a shape. Looking
at
![]() Young's Rule for
selecting class of projection
Young's Rule for
selecting class of projection
In 1920,
A.E. Young developed a formula for deciding when to use an azimuthal
projection. It works like this: suppose you draw two parallel lines—actually,
two parallel small circles on the earth's surface—that bound your area of
interest in the direction of its narrowest extent. These may be parallels of
latitude, but they may just as well be transverse or oblique lines. Call the
angular distance (the distance in degrees) between these lines δ.
Now measure the angular distance from the center of your area of interest to
the point farthest from the center. Call this value z. Young's rule says
that if z/δ is less than 1.41, an azimuthal projection is the most
suitable. If z/δ is greater than 1.41, you should use a conic or
cylindrical projection instead.
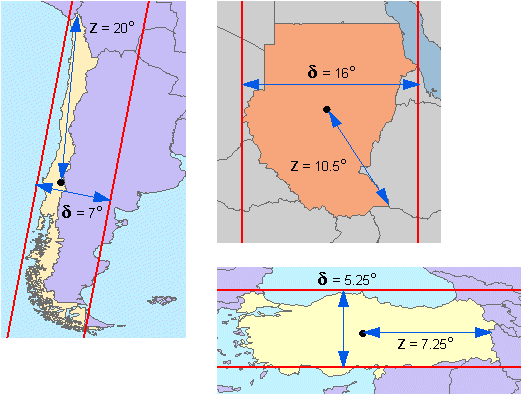
Country and
region outlines may have all sorts of protrusions, hollows, and weird dangling
appendages. Such irregularities may be small in area but have a large effect on
the spacing of your bounding parallel lines. You can adjust the value of δ
by deciding how far to respect these irregularities. Likewise, the value of z
is variable according to how you determine the center of the area of interest.
In ArcMap, for example, polygon centroids don't always fall within the polygon
boundary (
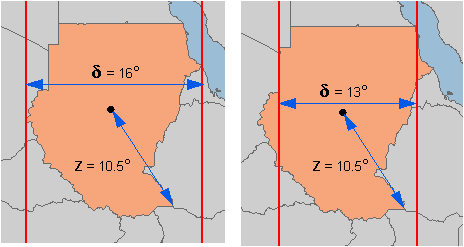
Left: The bounding
lines fully respect
Young's
rule tells you when to use an azimuthal projection versus a conic or
cylindrical projection, but it doesn't tell you how to choose between a conic
and a cylindrical when an azimuthal has been ruled out. To help make this
choice (repeating what was said above), look at the area of interest on a globe
and see if its longer axis more closely conforms to the arc of a great circle
or a small circle. Again, it's not always easy to tell, but a good look should
be enough to rule out a plainly bad choice.
![]() Using Young's Rule with
ArcMap
Using Young's Rule with
ArcMap
You can calculate z/δ in ArcMap with a little work:
1. Set the data frame to no projection
or to a geographic projection, such as WGS84. Note: Your display units
will default to decimal degrees. If no projection is set, ArcMap will perform
your subsequent measurements on a sphere. If a geographic projection is set,
the measurements will be done on a spheroid. (Either method should give good
results.)
2. Draw a pair of parallel graphic lines
that bound the area of interest as narrowly as possible.
3. Use the Measure tool ![]() to
measure the angular distance between the lines. This is δ. (Note:
Your graphic lines are lines—not parallel small circles—and may not have
constant angular distance between them. Therefore, make your δ measurement
across the center of the area of interest.)
to
measure the angular distance between the lines. This is δ. (Note:
Your graphic lines are lines—not parallel small circles—and may not have
constant angular distance between them. Therefore, make your δ measurement
across the center of the area of interest.)
4. Calculate the centroid of your area
of interest. (For help, see the ArcGIS online help topic Making field
calculations.) Note: If your area of interest includes two or more
polygons, you'll have to dissolve them.
5. Add a graphic point at the
centroid's coordinates. (Hint: Use the Size and Position tab of the graphic's
Properties dialog.)
6. Measure the angular distance from
the graphic point to the farthest boundary of the area of interest. This is z.
7. Calculate z /δ.
Recommended projections
After
taking into account the purpose of your map and the shape of your area of
interest, you should be able to narrow down the possibilities… if not to a
single projection, then at least to a short list of all good choices.
These
projections are among the best of their kind, but they are not a complete list
of suitable projections. With a few exceptions, these recommendations have been
taken from John Snyder, Map Projections: A Working Manual, pp. 34-35.
Recommended projections for
hemisphere maps
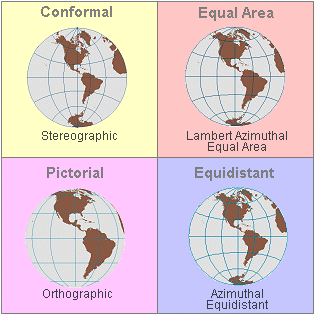
Recommended hemisphere
projections. The Orthographic projection does not preserve shape, area, or
distance, but it has a natural appearance and is often used for illustrations.
Recommended projections for maps of
continents and smaller areas
For equal area maps of
north-south and oblique extents, Snyder recommends transverse and oblique
aspects of the Cylindrical Equal Area. These aspects of the Cylindrical Equal
Area are not supported by ArcMap.
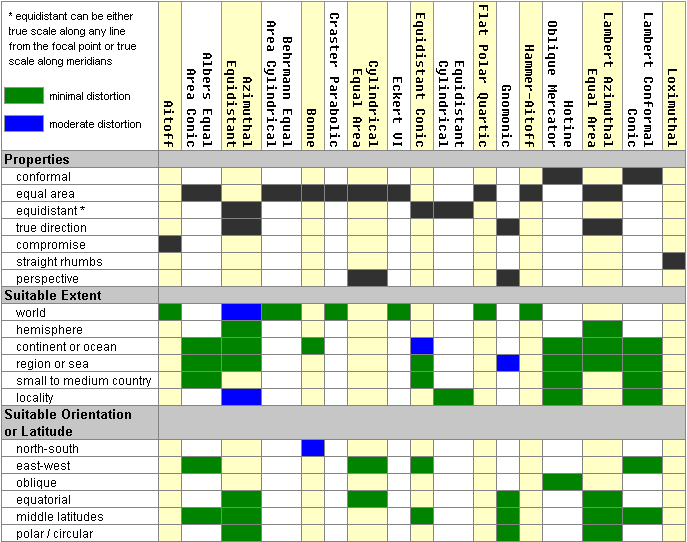
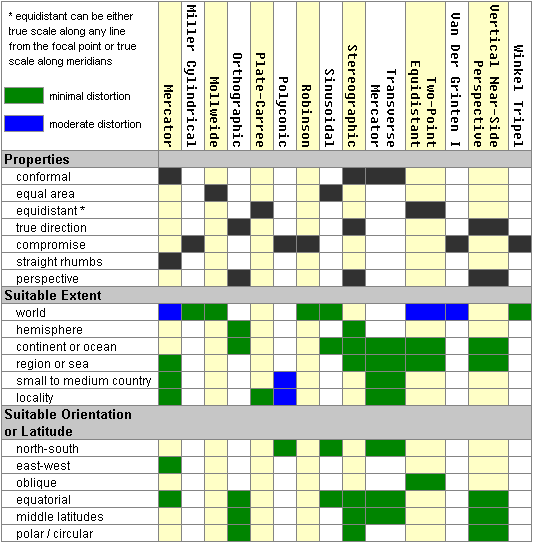
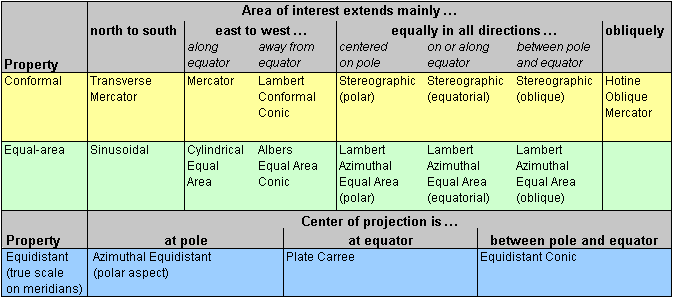
Projection properties summarized
The two
graphics below summarize properties for several popular projections. They are
adapted from the fold-out chart in Understanding Map Projections
(Kennedy, 1994-2000). This chart itself is adapted from a U.S. Geological
Survey poster called Map Projections.
Projection
names are listed across the top and projection properties along the side. The
properties include the spatial property preserved by the map; the projection's
appropriate extent (what size area it can cover); its appropriate spatial
orientation (for instance, areas lying east–west); and its appropriate zone
(for instance, mid-latitudes).
A black
square means that the projection preserves a spatial property. A green square
means the projection is highly suitable for a spatial extent or orientation. A
blue square means lower, but still acceptable, suitability.
Orientations
are a restriction on suitable extents. For example, if "continent" is
a suitable extent and "east–west" is a suitable orientation, it means
the projection is good for continents with an east–west orientation—not for all
continents plus all areas that lie east–west.