What is a datum transformation?
A datum
transformation is a set of math formulas that converts point coordinates from
one datum to another.
Datum
transformations take place in three-dimensional space, but you can get a sense
of how they work from a two-dimensional example. Suppose you have two different
maps of the same set of points. The differences between them can be expressed
in terms of linear distance, spatial orientation, and scale. The challenge is
to get the two sets of points into alignment—say, by aligning the points in
Datum 2 with the points in Datum 1. The datum transformation is the math you
use to do this.
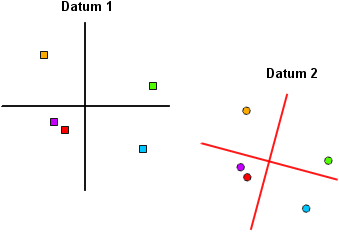
Two sets of points
representing the same locations on earth.
The first
step is to put the two sets of points into a common coordinate space.
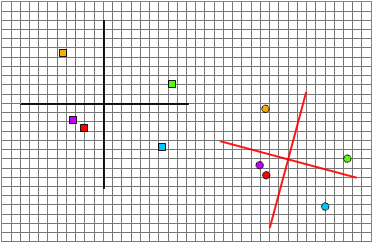
The systems are put
into common coordinate space.
Next, you
align the origins of the two systems by moving a certain number of units in the
x-direction and a certain number of units in the y-direction. Then you rotate
the axes into alignment. Finally, you apply a scale factor.
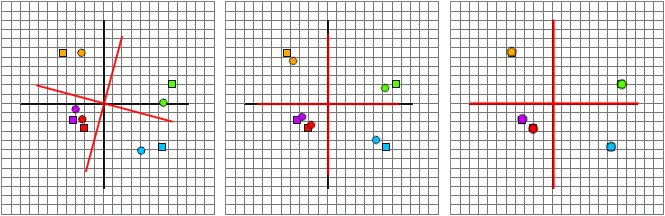
Left: the origins are
aligned, bringing the two sets of points into proximity. Center: the axes are
rotated, and the points almost match up. Right: the axes are scaled and the
transformation is complete.
The process
is similar in three-dimensional space except that you are working with a z-axis
as well as x- and y-axes. In a datum transformation, coordinates in both the
"from" datum and the "to" datum are converted from
latitude-longitude into three-dimensional cartesian
coordinate space. Next, the math is done to align the coordinates. Finally, the
coordinates are translated back into the latitude-longitude values of the
"to" datum.
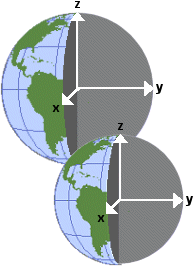
In the x,y,z coordinate system, the positive x-axis lies in the
plane of the equator and passes through 0° longitude; the positive y-axis lies
in the plane of the equator and passes through 90°E longitude; the positive
z-axis is parallel to the earth's rotation axis and passes through 90°N
latitude.
Datum transformation methods
Depending
on the "to" and "from" datums
involved, different transformation methods are used. In both the three- and
seven-parameter methods, the transformation aligns the x,y,z axes of the two datums
in three-dimensional cartesian coordinate space.
Three-parameter
methods
In a three-parameter transformation (also called a
geocentric translation), the axes of the two datums
are aligned using linear shifts of the x, y, and z axes of the datum being
transformed. A three-parameter transformation is appropriate when the x, y, and
z axes of the two datums are parallel and identically
scaled.
Seven-parameter
methods
A seven-parameter transformation is used when the axes
of the two datums are not parallel and identically
scaled. In addition to the three linear shift parameters, there are three
rotation parameters (one for each axis) and a scale factor.
NADCON
(grid-based) method
Another type of transformation, called a grid-based
transformation, is available for converting between the NAD27 and NAD83 datums. This type of transformation is more accurate than
the equation-based method described above. It relies on the fact that the exact
latitude-longitude differences between the two datums
have been calculated for thousands of control points.
Essentially
what happens in this transformation is that point coordinates on the
"from" datum (usually NAD27) are moved to the correct location on the
"to" datum simply by looking up the latitude and longitude
differences for that location in a table. The exact amount of shift hasn't been
calculated in advance for every point, of course, but every point does fall
within a grid cell which has bounding control points of known shift. The amount
of shift for a point within that cell can then be estimated by interpolation.
Molodensky method
The Molodensky method transforms the
latitude-longitude coordinates of the "from" datum directly to the
latitude-longitude coordinates of the "to" datum, thus skipping the
process of converting both datums into
three-dimensional cartesian
coordinates. It uses linear shifts of the x, y, and z axes of the
"from" datum's spheroid, plus the differences in the semi-major axes
and flattening ratios of the two spheroids.
Datum transformations in ArcGIS
When you
work with spatial data in ArcMap, you add data sets as layers to a data frame.
Every data set you add has a geographic coordinate system associated with it,
describing the data's latitude-longitude coordinates. If the data set is
already in a map projection, then it is also associated with a projected
coordinate system, describing the projection and its parameters. The geographic
coordinate system is still there, however—lurking below the surface, so to
speak.
A data frame is not inherently associated with a coordinate system, but it
adopts the coordinate system—the
If a layer
has the same
If,
however, the layer has a different
The process
of matching the coordinate systems of layers to the coordinate system of the
data frame has many permutations, summarized in the following table.
|
Data frame's coordinate system |
Layer's coordinate system |
Operation needed |
|
|
|
None |
|
|
|
None; ArcMap "unprojects"
the layer on the fly |
|
|
|
Datum transformation from |
|
|
|
Datum transformation from |
|
|
|
On-the-fly projection of layer to |
|
|
|
None |
|
|
|
On-the-fly reprojection of layer to |
|
|
|
Datum transformation from |
|
|
|
Datum transformation from |
|
|
|
Datum transformation from |