What is a datum?

Suppose you have a pair of latitude-longitude coordinates, such as the following:

77° 2' 59.51'' W
38° 53' 20.95'' N

Do these coordinates specify a single, definite point on earth?

The answer really depends on how you interpret the question. A pair of latitude-longitude coordinates, like the ones in the question above, do uniquely identify a point on earth within the context of a particular geographic coordinate system. But they don't identify a single point absolutely—that is, if you change some of the settings of your geographic coordinate system, the same pair of coordinates will mark a different place on the earth.

Imagine two geographic coordinate systems. Both are measured in degrees, so their coordinate values are + or - 90 N/S and + or - 180 E/W. And both define the Greenwich meridian to be 0 longitude. Yet in one of them the coordinates 77° 2' 59.51'' W, 38° 53' 20.95'' N mark the Lincoln Memorial in Washington, D.C., while in the other system they mark a spot in the Potomac River.

How can that be? A number of factors can make it happen. For example, it can happen if the two geographic coordinate systems are associated with different spheroids. (You saw an example of this in the very first exercise of the course, when you looked at the coastline of Long Island mapped on three different spheroids.) In the next concept, we'll look at some of the other factors that can cause this to happen, but for the moment let's just give all these factors collectively the name of "datum." To give a general answer to the question, "What is a datum?," we might say a datum is the list of factors, or initial specifications, that explains why the latitude-longitude coordinates in one geographic coordinate system identify different points on earth than the very same coordinates in another system.

That sounds a little abstract, but the basic idea isn't hard. Suppose you and I both make a chocolate mousse, using the same ingredients and working in the same kitchen. Nevertheless, our mousses come out tasting different. Why? Well, even though we used the same ingredients, maybe we didn't follow exactly the same recipe. You can think of a datum as something like the recipe for a geographic coordinate system.

Components of a datum

In the previous module, you learned that a geographic coordinate system has three components: an angular unit of measure, a prime meridian, and a datum. The first two are familiar to you, so now let's look at the third. Datums are an interesting subject, but for practical purposes, you don't really need to know all the details that are presented here—what matters most is knowing which datum you're working with, not exactly how it's been defined.

The first element of a datum is one we've already mentioned—the parameters of the spheroid used to model the earth.

Refresh your memory on the dimensions of a spheroid

A spheroid can be defined by the length of its semi-major and semi-minor axes, or by the length of its semi-major axis and a flattening value. (Flattening is the ratio of the semi-major to the semi-minor axis.)

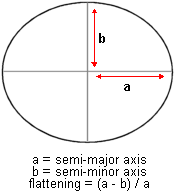
The dimensions of a spheroid.

To get at the second element, we have to consider a new idea. In the topic introduction, you learned that the earth is best represented by a model called the geoid, but that this model has an irregular shape. Therefore, coordinate systems are applied to the simpler model of a spheroid. The problem is that actual measurements of location (whether made by ground survey or satellite) conform to the geoid surface and have to be mathematically recalculated to positions on the spheroid. This process changes the measured positions of many points—sometimes by a few meters, sometimes by hundreds of meters. It's an unavoidable compromise. To get the mathematical convenience of a spheroid, you have to give up some positional accuracy.

Which points are affected? It depends. Different datums use a different orientation of the spheroid to the geoid to determine which parts of the world keep accurate coordinates on the spheroid. For an area of interest, the surface of the spheroid can arbitrarily be made to coincide with the surface of the geoid; for this area, measurements can be accurately transferred from the geoid to the spheroid. The drawback is that in other areas the geoid and the spheroid will not match up. In these areas, point coordinates have to be adjusted (with loss of accuracy) when they are moved from the geoid to the spheroid.

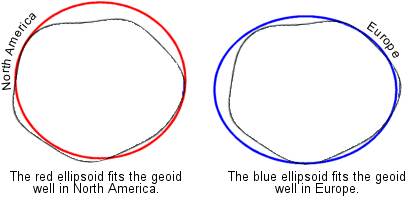
Left: the spheroid is oriented to the geoid to preserve accurate measurements for North America. Right: the spheroid is oriented to preserve accurate measurements for Europe. The problems of orienting the spheroid to the geoid and choosing a spheroid are interrelated, since a single spheroid does not fit all parts of the geoid equally well.

So the first element of a datum is the spheroid dimensions, and the second is the orientation of the spheroid to the geoid. The third element is the datum origin. This is a point whose latitude-longitude coordinates on the spheroid are true to the geoid, whose coordinates are not subject to adjustment, and to whose coordinates all other points in the system are ultimately referred. The fourth element is an azimuth value from the origin to a second point. As with the origin, this azimuth measurement is preserved from the geoid to the spheroid. It ultimately determines how the entire system of points is spatially oriented with respect to the lines of latitude and longitude on the spheroid.

This may seem like a lot to digest, but you don't really need to remember it all (at least not beyond the module exam). What you should remember is that changes to the values of any datum parameters can result in changes to coordinate values of points. It follows from this that if you have two different datums, you also have two different geographic coordinate systems.

Once again, the elements of a datum are:

· a spheroid

· an initial reference point, or origin

· an azimuth from the origin to a second point

· the orientation of the spheroid to the geoid (This is defined as the distance separating the geoid and the spheroid at the origin, and it is usually zero.)

Horizontal and vertical datums

Horizontal datums—the kind we've been talking about here—are the reference values for a system of location measurements. Vertical datums, by contrast, are the reference values for a system of elevation measurements. The job of a vertical datum is to define where zero elevation is—this is usually done by determining mean sea level, a project that involves measuring tides over a cycle of many years.

Local and earth-centered datums

Datums, as described in the previous concept, are called local datums because they preserve accurate point coordinates for a certain region, such as North America or Europe. The coordinates of the entire set of points based on such a datum are determined by ground-based survey equipment and triangulation—all with reference to the initially-accepted coordinates of the origin.

How are the coordinates of the origin determined?

Latitude is determined by measuring angles to stars (in particular, the North Star) and longitude is determined by comparing local time to Greenwich time.

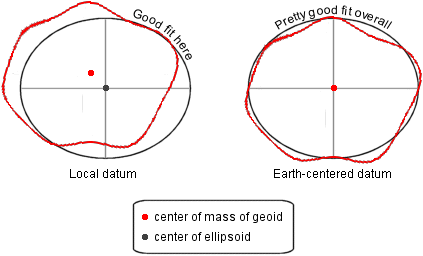
Left: in a local datum, the spheroid matches the geoid closely in one part of the world and is quite a bit off in others. The geoid's center of mass does not align with the center of the spheroid. Right: in an earth-centered datum, the spheroid matches the geoid pretty closely all around the world, but nowhere perfectly-except at their centers.

Which type of datum is better? It depends on your needs. An earth-centered datum is better for mapping the world; a local datum is better for mapping a small piece of it. Earth-centered datums, in particular WGS84, are becoming a standard because they work equally well for everyone, but local datums will be around for a long time to come.

Elements of an earth-centered datum

The elements of an earth-centered datum are different from those of a local datum (except that both specify an spheroid). That's because the measurement technology is so different. Without going into a description of satellite geodesy—which is complicated—it doesn't really make sense to list the particulars of earth-centered datums. To try to stuff it into a paragraph, we can say that the basic principle of satellite geodesy is triangulation (same as earth-based surveying) and involves locating points on earth in terms of how long it takes a ground station to receive radio signals from different satellites. Consequently, the elements of an earth-centered datum are things like satellite positions, the speed of light, and synchronization values between satellite clocks and earth clocks.

Common datums

Local datums

North American Datum of 1927 (NAD27)
Well-suited to the United States, Canada, Mexico, and the Caribbean. (It has since been improved on by the earth-centered North American Datum of 1983.)

European Datum of 1950 (ED50)
Well-suited to the countries of continental Europe.

Tokyo Datum
Well-suited to Japan.

Indian Datum
Well-suited to India and nearby southeast Asian countries.

Datum	Origin	Origin coordinates	Spheroid used
NAD27	Meades Ranch, Kansas	33° 13' 26.686" N 98° 32' 30.506'' W	Clarke 1866
ED50	Potsdam, Germany	52° 22' 51.45" N 13° 03' 58.74" E	International 1924
Tokyo	Tokyo Observatory	35° 39' 17.51" N 139° 44' 40.50" E	Bessel
Indian	Kalianpur, India	24° 07' 11.26" N 77° 39' 12.57" E	Everest

Earth-centered datums

World Geodetic System of 1984 (WGS84)
The datum on which GPS coordinates are based and probably the most common datum for GIS data sets with global extent.

Soviet Geodetic System of 1990 (SGS90)
Similar to WGS84, this is the datum on which GLONASS coordinates are based. (GLONASS, or the Global Navigation Satellite System, is Russia's counterpart to the GPS system.)

North American Datum of 1983 (NAD83)
NAD83 is a correction of NAD27 coordinates that is based on both earth and satellite measurements. Unlike NAD27, however, it is an earth-centered datum, not a local datum. Its coordinates are very similar to WGS84 coordinates and can be used interchangeably with them.

Datum transformations

As you saw in the last topic, different datums lead to different coordinate values for point locations. It follows that you'll run into problems if you try to combine data sets that are based on different datums. You've probably seen this for yourself in situations where two layers don't line up like they should.

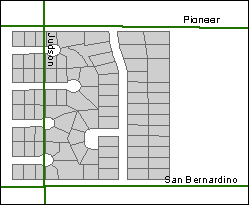
The streets and parcels don't align because they are based on different datums. The result is that a street runs through some parcels.

In this topic, you'll see how problems like this can be resolved through datum transformations. In the exercises, you'll get lots of practice applying datum transformations in ArcMap. (You'll also get a better understanding of those pesky warning messages that pop up whenver you add layers based on different datums.)

In this module, the terms "datum transformation" and "geographic coordinate system transformation" are used interchangeably. Transforming a datum also transforms the geographic coordinate system of which it is a part.